Article – New Year’s Eve: Champagne, Lotteries, and the Science of Probability

Happy New Year!!

New Year’s Article – 2025!

Champagne, Lotteries and the Science of Probability

by Ian Sherrington

Series – The Online Gambling Industry
The Paperwork – Jurisdictions, Legal and Compliance

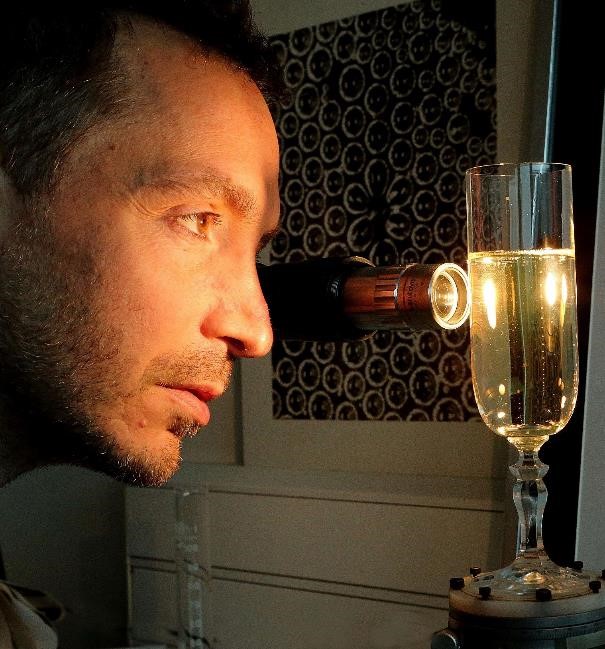
Lovely Bubbly!

Champagne: Random Bubbles

Champagne, the quintessential drink of celebration, owes its festive sparkle to the science of bubbles. When a bottle is uncorked, dissolved carbon dioxide escapes the liquid in the form of bubbles, creating a mesmerizing dance that captivates the eye.

The path of each bubble as it rises is influenced by countless factors: microscopic imperfections in the glass, variations in temperature, and the liquid’s viscosity. This randomness ensures that no two glasses of champagne sparkle exactly alike.

From a scientific perspective, the behavior of these bubbles can be described by probability. Researchers have found that the size and speed of bubbles follow predictable distributions, even though their individual journeys seem random. This interplay of order and chaos mirrors the essence of probability itself—a tool to understand patterns in seemingly unpredictable phenomena.

Latest Articles

New Year’s Article – Champagne, Lotteries and the Science of Probability

Interview – Gyneth McAllister, MBA

AI Football Match Analysis

Betting Jobs News Interview

SiGMA Magazine

Gérard Liger-Belair

The Science of Bubbles

Gérard Liger-Belair, a physicist with a passion for uncovering the mysteries of effervescence, has dedicated his career to the study of champagne bubbles. His fascination began in 1999 when he observed the mesmerizing rise of bubbles in a glass of beer, sparking an interest that led him to explore the micro-mechanics of carbonation.

After initial independent research, he partnered with major champagne producers like Moët & Chandon, eager to understand the science behind their iconic product. Gérard’s work at the University of Reims in the heart of the Champagne region has spanned over 15 years, during which he has pioneered the study of champagne’s bubbles through high-resolution imaging and meticulous experimentation.

His findings highlight help to explain how the science of bubbles enhances our appreciation of champagne’s unique bubblyness.

Lovely Bubbly!

Fascinating Facts Behind Champagne’s Bubbles!

Champagne’s effervescent charm is deeply tied to the science of its bubbles, which enhance the drink’s flavor, aroma, and celebratory experience. Here are some key insights into champagne’s bubbles:

CO2 Retention and Pouring Techniques: A typical bottle contains enough CO2 to create 20 million bubbles. Up to 80% of CO2 escapes when the cork pops, so easing off the cork and tilting the glass during pouring preserves more bubbles.

Bubble Formation: Bubbles emerge from microscopic fibers or imperfections in the glass. In a standard glass, bubbles form at a rate of 400 per second, compared to beer’s 150 per second.

Flavor and Aroma Enhancement: As bubbles burst, they eject tiny droplets into the air, amplifying champagne’s aromas and flavors.

Optimal Glass Shape: Traditional flutes and coupes are suboptimal. Flutes concentrate CO2, irritating the nose, while coupes dilute aromas. Wine glasses balance the bubbles’ ability to enhance taste and aroma.

Bubble Size and Taste: Smaller bubbles, often prized, result from lower sugar levels during fermentation, leading to drier champagne. Flutes produce larger bubbles than coupes due to the sheer liquid weight: the smaller the liquid level in the glass, the smaller the bubbles.

Magnum Bottles and Bubble Preservation: Larger bottles like magnums better retain bubbles due to a higher liquid volume and less CO2 escape through the cork.

From Bubbles to Probability: The Mathematics Behind the Sparkle

The seemingly unpredictable rise of champagne bubbles offers a glimpse into the deeper workings of probability. At first glance, the bubbles seem chaotic and without pattern, much like the events of daily life. Yet, when studied collectively, they reveal predictable trends and distributions—a hallmark of probability theory.

When analyzed on a large scale, they demonstrate clear patterns governed by probability. For example, the rate at which bubbles emerge, their size distribution, and the frequency of bursts follow statistical trends. These patterns result from consistent physical factors like temperature, glass imperfections, and the CO₂ concentration in the liquid.

Probability theory excels at finding order in seemingly chaotic systems such as bubble formation.

It was Blaise Pascal, alongside Pierre de Fermat, who laid the groundwork for modern probability theory in the 17th century. What began as a mathematical inquiry into games of chance evolved into a profound tool for studying the randomness of the world.

Blaise Pascal, born June 19, 1623 in Clermont-Ferrand, France.

Blaise Pascal – A Pioneer in Mathematics and Philosophy

Blaise Pascal, a 17th-century French mathematician, physicist, and philosopher, is widely regarded as one of the founding figures of probability theory. His collaboration with Pierre de Fermat in 1654 to solve problems related to gambling games marked the birth of this mathematical field. Their correspondence addressed questions such as how to fairly divide stakes in an interrupted game—a problem now known as the “problem of points.”

The “problem of points” involves determining how to fairly split the stakes of a game if it is halted before its conclusion. For example, consider two players engaged in a game where the first to win three rounds claims the pot. If the game is interrupted with one player having won two rounds and the other one round, how should the pot be divided?

Pascal and Fermat solved this by considering the possible outcomes of the remaining rounds, calculating the proportion of chances each player had of ultimately winning the game. This approach to breaking down complex scenarios into probabilities formed the foundation for modern decision theory, risk analysis and ultimately the online gambling industry.

Pierre de Fermat – A Mathematical Luminary

Pascal’s partner in developing probability theory, Pierre de Fermat, was an equally brilliant mathematician whose work left an indelible mark on mathematics. Fermat is perhaps best known for Fermat’s Last Theorem. Bear with me for a bit o’ mathematics. His theorem (or statement) says:

There are no three positive integers $\text{a, b}$ and $\text{c}$ that satisfy the equation $a^n + b^n = c^n$ for any integer $n > 2$

That means when $n = 1$ or $n = 2$ , there are solutions, but not when $n$ is greater than $2$ . As $n > 2$ is infinite, how do you prove Fermat Theorem is correct?

Although Fermat famously claimed to have a proved his own theorem, he said the proof was “too large to fit in the margin” of his notebook.

The theorem remained unproven for over 350 years until British mathematician Andrew Wiles solved it in 1994.

Fermat’s contributions extended beyond this theorem; he also worked on analytic geometry, calculus, and number theory, laying the groundwork for modern mathematics.

Pascal’s Wager – Betting on God

Does God exist? It’s a good bet!

Pascal’s Wager: Betting on God

Pascal was not only a brilliant mathematician, but was also a philosopher. The two subjects blurred into each other when Pascal mused the chances of God’s existence.

Pascal’s Wager addresses the question of whether it is rational to believe in God, even without definitive proof of His existence.

Pascal argued that humans face two choices: to believe in God or not. Each choice carries potential consequences!

If God exists and you believe, the reward is infinite (eternal happiness in heaven).
If God exists and you do not believe, the loss is infinite (eternal damnation).
If God does not exist and you believe, the cost is finite (a life lived in faith without a divine reward).
If God does not exist and you do not believe, the gain or loss is also finite.

From this perspective, Pascal reasoned that belief in God is the safer and more rational choice, as it offers the potential for infinite gain with minimal risk.

My Night at Maud’s

The 1969 French film My Night at Maud’s, directed by Éric Rohmer, beautifully captures Pascal’s multifaceted legacy. The movie follows Jean-Louis, a devout Catholic engineer, who engages in a philosophical debate with Vidal, a Marxist lecturer, and Maud, a free-spirited divorcee. The characters discuss topics like faith, morality, and Pascal’s Wager, reflecting on the interplay between reason and belief.

A pivotal scene involves a debate about the rationality of belief in God, directly referencing Pascal’s Wager. The film’s exploration of decision-making under uncertainty echoes Pascal’s work in probability, making it a thought-provoking study of human choices.

This pragmatic approach to faith aligns with the principles of probability, weighing outcomes based on their likelihood and impact. While the Wager does not attempt to prove God’s existence, it provides a framework for making decisions under uncertainty, resonating with themes central to both probability theory and gambling.

Probability is at the heart of the gambling industry

Probability: Fundamental Knowledge for Gambling

Probability and odds are central concepts in the world of gambling, shaping how games are played and how bets are placed.

What is Probability?

Probability is a measure of how likely an event is to occur. It is usually expressed as a number between 0 and 1, where 0 means the event will not happen, and 1 means the event will certainly happen. The formula for calculating probability

$\text{Probability} = \dfrac{\text{Winning outcomes}}{\text{Total possible outcomes}}$

For example, in a fair coin toss, there are two possible outcomes: heads or tails. The probability of getting heads is:

$\text{Probability of Heads} = \frac{1}{2} = 0.5$

In gambling, probability helps to assess how likely a specific outcome is in a game. This can apply to rolling dice, drawing cards, or even betting on sports.

Odds are that you know this already!

How does Probability relate to Odds?

Odds are a way of expressing the likelihood of an event occurring, but they are presented in a different format than probability. Odds are usually written as a ratio of two numbers. There are three common types of odds used in the gambling world. these are:

Fractional Odds: These are often used in sports betting and represent the ratio of the amount you can win relative to the stake. For example, odds of 5/1 mean you can win $5 for every $1 you bet.
- If you bet $10 at 5/1 odds, you would win $50 if the bet is successful.
Decimal Odds: These are common in European betting and represent the total payout (including your stake) for each dollar bet. For example, decimal odds of 6.00 mean that for every $1 wagered, the total payout will be $6.
- If you bet $10 at 6.00 odds, you would receive $60 (your $10 stake plus $50 in winnings).
American Odds: See the detail box below.

American Odds Format

American Odds

Also known as moneyline odds, American Odds are commonly used in sports betting in the United States.

They can appear as either positive (+) or negative (-) numbers, and they indicate how much a bettor can win or needs to bet in order to make a profit. Understanding how American odds work is crucial for anyone involved in sports betting.

Positive American Odds (+)

Positive American odds show how much profit that can be made on a $100 bet. They are typically used to represent underdogs in a match.

Example: +200

A bet of $100 on odds of +200 will win $200 if the bet is successful, in addition to getting back the original $100 wagered.
In other words, for every $100 bet, the win is $200 (if the bet wins).
The formula for calculating the potential payout is:
(1) $\begin{equation*}\text{Payout} = (\frac{\text{Odds}}{100}) \times \text{Bet}\end{equation*}$

So, with +200 odds:
(2) $\begin{equation*}\text{Payout} = (\frac{200}{100}) \times 100 = 200\end{equation*}$

The total payout will be $300 (the original bet of $100 plus $200 in winnings).

Negative American Odds (-)

Negative American odds indicate how much you need to bet in order to win $100. They are typically used to represent favorites in a match, as the favored team or player is more likely to win.

Example: -150

A bet of $150 on odds of -150 will win $100 if the bet is successful, in addition to getting back the original $150 wagered.
In other words, to win $100, the bet would need to be $150.
The formula for calculating the potential payout is:
(3) $\begin{equation*}\text{Payout} = (\frac{100}{\text{Odds}}) \times \text{Bet}\end{equation*}$

So, with -150 odds:
(4) $\begin{equation*}\text{Payout} = (\frac{100}{\text{150}}) \times 150 = 100\end{equation*}$

The total payout will be $250 (the original bet of $150 plus $100 in winnings).

How to Convert American Odds to Probability

American odds can also be converted into implied probability, which helps you understand the likelihood of an event happening based on the odds.

Positive Odds (+): To convert positive odds to implied probability, use the following formula:
$\text{Implied Probability} = \frac{100}{\text{Odds} + 100}$
Example for +200
$\text{Implied Probability} = \frac{100}{200 + 100} = 0.3333 \text{ or } 33.33\%$
Negative Odds (-): To convert negative odds to implied probability, use this formula
$\text{Implied Probability} = \frac{\text{Absolute Value of Odds}}{\text{Absolute Value of Odds} + 100}$

Example for -150
$\text{Implied Probability} = \frac{150}{150 + 100} = 0.6 \text{ or } 60\%$

Relationship Between Probability and Odds

Probability and odds are closely related, and you can convert between the two. Here’s how:

From Odds to Probability: To convert fractional odds into probability, use the formula:

$\text{Probability} = \frac{\text{Denominator of the odds}}{\text{Denominator of the odds} + \text{Numerator of the Odds}}$

For example, with odds of 5/1:
$\text{Probability} = \frac{1}{5 + 1} = \frac{1}{6} = 0.1667 \text{ or } 16.67%$
From Probability to Odds: To convert probability into odds, use the formula:

$\text{Odds} = \frac{1 - \text{Probability}}{\text{Probability}}$

For example, if the probability of an event is 0.25 (25%), the odds would be:
$\text{Odds} = \frac{1 - 0.25}{0.25} = \frac{0.75}{0.25} = \text{3/1}$

House Edge and How It Affects the Game

In most gambling games, the house (casino or bookmaker) has an advantage, known as the house edge. This means that, on average, players are more likely to lose than win. The house edge is built into the odds offered by the casino, making it less likely that a player will win in the long run.

For example, in a game of roulette, the odds of winning a single number bet are 37/1 in European roulette (because there are 37 pockets: 1 to 36 plus a single zero). However, the payout for winning is only 35/1, which gives the house an edge.

The bookmaker’s margin (also called the “overround” or “vig”) represents the profit margin that a bookmaker builds into their odds. It ensures that, regardless of the outcome of an event, the bookmaker expects to make a profit.

Bookmakers do not offer “fair odds” (which are based solely on the true probabilities of outcomes) because doing so would eliminate their profit. Instead, they adjust the odds to ensure that the total implied probabilities exceed 100%.

The margin can be calculated using the implied probabilities of all outcomes.

Formula for Implied Probability:

The implied probability for decimal odds $O$ is calculated as: $P=\dfrac{1}{O}$

where:

$P$ is the implied probability (in decimal form).
$O$ is the decimal odds for an outcome.

Formula for the Bookmaker’s Margin:

If there are $n$ possible outcomes, the bookmaker’s margin $M$ is:

$M = \left( \sum_{i=1}^{n} \dfrac{1}{O_i} \right) - 1$

Where $.O_i$ is the decimal odds for the $i$ th outcome
$n$ is the total number of outcomes.

Don’t panic! For a simple football match, the margin calculation break down simply as in this example:

Luton Town (Win): $O_1=2.5$ Draw: $O_2=3.4$ Norwich City (Win): $O_3=2.7$

Substitute these into the formula:

$M= \left( \dfrac{1}{2.5} + \dfrac{1}{3.4} + \dfrac{1}{2.7} \right) - 1$

Simplifying each term

$\frac{1}{2.5} = 0.4, \quad \frac{1}{3.4} \approx 0.2941, \quad \frac{1}{2.7} \approx 0.3704$

Adding these together gives us the probability, (which has a value of 1 for a sure thing, so a value exceeding $1$ will give us the margin)

$\sum_{i=1}^{3} \dfrac{1}{O_i} = 0.4 + 0.2941 + 0.3704 = 1.0645$

The value is greater than $1$ . The margin is calculated by subtracting $1$

$M =1.0645 - 1 = 0.0645$

Express as a percentage Convert to a percentage:

$M \times{100} = 6.45\%$

Final Answer:

The bookmaker’s margin for these odds is 6.45%.

Lotteries: Dreams Built on Probability

Lotteries are a cornerstone of New Year’s traditions in many parts of the world, offering participants the tantalizing hope of sudden wealth. From Spain’s famous El Gordo to massive global jackpots, the allure of lotteries is universal. In 2024 alone, it’s estimated that worldwide lottery ticket sales for the holiday season will exceed $120 billion—a testament to their enduring appeal.

At the heart of every lottery lies probability. When you buy a ticket, you’re participating in a system governed by precise mathematical rules. For example, the odds of winning the Powerball jackpot are approximately 1 in 292 million. These figures might seem daunting, but they are a direct application of probability theory.

Probability doesn’t just define the chances of winning; it also shapes the design of lotteries. By carefully balancing the size of the jackpot, the cost of tickets, and the odds of winning, organizers create a system that maximizes participation while ensuring profitability. This delicate balance wouldn’t be possible without the mathematical insights pioneered by Pascal and his contemporaries.

Yet, people continue to play (thank goodness), driven by the hope that they might defy the odds. This hope is rooted in the human tendency to dream big—to imagine that, against all statistical likelihood, they could hold the winning ticket. In this way, lotteries capture both the rational and emotional sides of probability, blending mathematical structure with the thrill of possibility.

As we enter the New Year, lottery tickets symbolize more than just a chance at wealth. They represent our willingness to take risks, to embrace uncertainty, and to hope for a brighter future.

It’s not all about mathematics

Confucius, the I Ching, and the Wisdom of Randomness

Long before Blaise Pascal developed probability theory, ancient Chinese philosophy explored randomness and its deeper meanings through the I Ching, or the Book of Changes. This revered text, dating back over 3,000 years, provides a framework for understanding life’s uncertainties and the hidden patterns within apparent chaos.

The I Ching and Its Philosophical Roots

The I Ching is based on the concept of constant change, driven by the interplay of opposing forces, yin and yang. These dualities represent the dynamic balance of life—light and dark, order and disorder, certainty and uncertainty.

By consulting the I Ching, individuals seek insight into how these forces shape their lives and guide their decisions.

The Yarrow Stalk Method: Randomness with Meaning

Traditionally, the I Ching was used with 50 yarrow stalks. Through a meticulous process of dividing and counting the stalks, users would generate one of 64 hexagrams, each composed of six lines (either broken or unbroken). The randomness in this process mirrors the unpredictability of life events, while the resulting hexagrams offer symbolic guidance on navigating life’s complexities.

Modern interpretations often use coin tosses for simplicity, but the principle remains the same: random outcomes are imbued with meaning through interpretation. This practice highlights a unique perspective on randomness—not as pure chaos, but as a reflection of a deeper order waiting to be uncovered.

Check this YouTube video for the best description of how to use the I Ching that I can find. Unfortunately the author does not allow his superb video to be embedded into external web pages, so it will open in a new window.

Confucius, one of China’s most influential philosophers, deeply respected the I Ching and its teachings. He saw it not merely as a tool for divination but as a source of moral and philosophical wisdom. For Confucius, the randomness of the yarrow stalks symbolized the unpredictability of life, while the hexagrams provided a framework for understanding one’s place within the cosmic order.

Conclusion: Embracing Chance

As the New Year begins, we celebrate both the chaos and the order of life.

The expectant rise of champagne bubbles, the hopeful purchase of a lottery ticket, or the contemplative wisdom of the I Ching, these practices remind us that randomness is something to embrace.

The science of probability offers us tools to understand the unpredictable, yet it also invites us to appreciate the beauty of uncertainty. From Blaise Pascal’s groundbreaking theories to the ancient reflections of Confucius, the study of chance has continually shown us that within randomness lies meaning, and within uncertainty lies opportunity.

As we toast to another year, let us celebrate not only the traditions of the season but also the deeper truths they reveal. For in the unpredictability of life, we find endless reasons to dream, to hope, and to believe in the possibilities of a better tomorrow.

Happy New Year!

Home